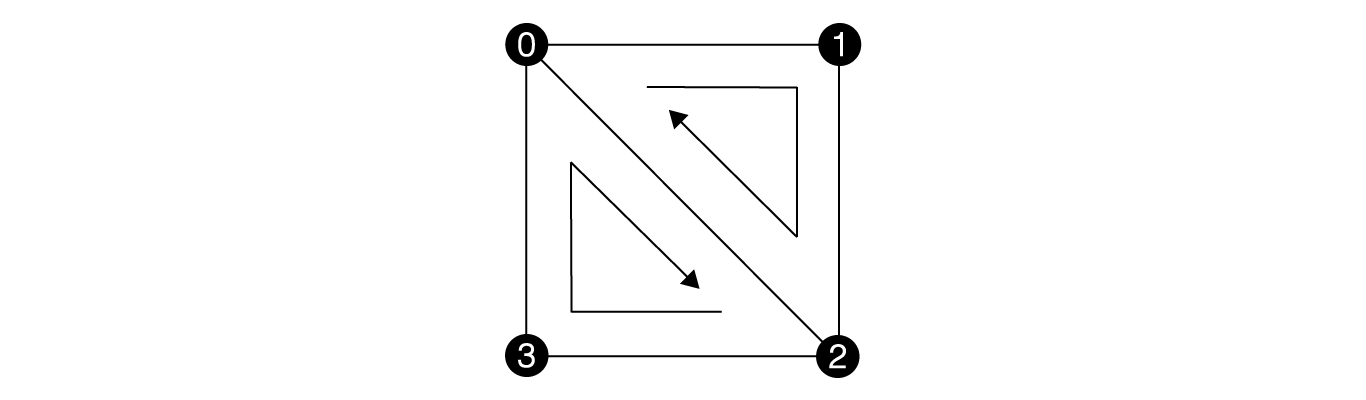
図1.1: Quadモデルの構造 黒丸はモデルの頂点を表し、黒丸内の0〜3の数字は頂点のindexを示している 矢印は一枚の三角形を構築する頂点indexの指定順(右上は0,1,2の順番で指定された三角形、左下は2,3,0の順番で指定された三角形)
プロシージャルモデリング(Procedural Modeling)とは、ルールを利用して3Dモデルを構築するテクニックのことです。モデリングというと、一般的にはモデリングソフトであるBlenderや3ds Maxなどを利用して、頂点や線分を動かしつつ目標とする形を得るように手で操作をしていくことを指しますが、それとは対象的に、ルールを記述し、自動化された一連の処理の結果、形を得るアプローチのことをプロシージャルモデリングと呼びます。
プロシージャルモデリングは様々な分野で応用されていて、例えばゲームでは、地形の生成や植物の造形、都市の構築などで利用されている例があり、この技術を用いることで、プレイするごとにステージ構造が変わるなどといったコンテンツデザインが可能になります。
また、建築やプロダクトデザインの分野でも、Rhinoceros*1というCADソフトのプラグインであるGrasshopper*2を使って、プロシージャルに形状をデザインする手法が活発に利用されています。
[*1] http://www.rhino3d.co.jp/
[*2] http://www.grasshopper3d.com/
プロシージャルモデリングを使えば以下のようなことが可能になります。
パラメトリックな構造とは、あるパラメータに応じて構造が持つ要素を変形させられる構造のことで、例えば球(Sphere)のモデルであれば、大きさを表す半径(radius)と、球の滑らかさを表す分割数(segments)といったパラメータが定義でき、それらの値を変化させることで望むサイズや滑らかさを持つ球を得ることができます。
パラメトリックな構造を定義するプログラムを一度実装してしまえば、様々な場面で特定の構造を持つモデルを欲しい形で得ることができ、便利です。
前述の通り、ゲームなどの分野においては、地形や樹木の生成にプロシージャルモデリングが利用される例はとても多く、一度モデルとして書き出されたものを組み込むのではなく、コンテンツ内でリアルタイムに生成されることもあります。リアルタイムなコンテンツにプロシージャルモデリングのテクニックを利用すると、例えば太陽に向かって生える木を任意の位置に生成したり、クリックした位置からビルが立ち並んでいくように街を構築したりするようなことが実現できます。
また、様々なパターンのモデルをコンテンツに組み込むとデータサイズが膨らんでしまいますが、プロシージャルモデリングを利用してモデルのバリエーションを増やせば、データサイズを抑えることができます。
プロシージャルモデリングのテクニックを学び、プログラムによってモデルを構築していくことを極めていけば、モデリングツールそのものを自分で開発することも可能になるでしょう。
Unityでは、モデルの形を表すジオメトリデータをMeshクラスによって管理します。
モデルの形は3D空間に並べられた三角形から構成されていて、1つの三角形は3つの頂点により定義されます。モデルが持つ頂点と三角形データのMeshクラスでの管理方法について、Unityの公式ドキュメントで以下のように解説されています。
Meshクラスでは、すべての頂点はひとつの配列に格納されていて、それぞれの三角形は頂点配列のインデックスにあたる3つの整数により指定されます。三角形はさらに1つの整数の配列として集められます。この整数は配列の最初から3つごとにグルーピングされるため、要素 0、1、2は最初の三角形を定義し、2つ目の三角形は3、4、5と続いていきます。*3
[*3] https://docs.unity3d.com/jp/540/Manual/AnatomyofaMesh.html
モデルには、それぞれの頂点に対応するように、テクスチャマッピングを行うために必要なテクスチャ上の座標を表すuv座標、ライティング時に光源の影響度を計算するために必要な法線ベクトル(normalとも呼ばれます)を含められます。
本章ではhttps://github.com/IndieVisualLab/UnityGraphicsProgrammingリポジトリ内にあるAssets/ProceduralModeling以下をサンプルプログラムとして用意しています。
C#スクリプトによるモデル生成が主な解説内容となるため、Assets/ProceduralModeling/Scripts以下にあるC#スクリプトを参照しつつ、解説を進めていきます。
本章のサンプルコードはUnity5.0以上で動作することを確認しています。
基本的なモデルであるQuadを例として、モデルをプログラムから構築する方法を解説していきます。Quadは4つの頂点からなる2枚の三角形を合わせた正方形モデルで、UnityではPrimitive Meshとしてデフォルトで提供されていますが、最も基本的な形状であるため、モデルの構造を理解するための例として役立ちます。

図1.1: Quadモデルの構造 黒丸はモデルの頂点を表し、黒丸内の0〜3の数字は頂点のindexを示している 矢印は一枚の三角形を構築する頂点indexの指定順(右上は0,1,2の順番で指定された三角形、左下は2,3,0の順番で指定された三角形)
まずはMeshクラスのインスタンスを生成します。
// Meshのインスタンスを生成 var mesh = new Mesh();
次にQuadの四隅に位置する4つの頂点を表すVector3配列を生成します。また、uv座標と法線のデータも4つの頂点それぞれに対応するように用意します。
// Quadの横幅と縦幅がそれぞれsizeの長さになるように半分の長さを求める
var hsize = size * 0.5f;
// Quadの頂点データ
var vertices = new Vector3[] {
new Vector3(-hsize, hsize, 0f), // 1つ目の頂点 Quadの左上の位置
new Vector3( hsize, hsize, 0f), // 2つ目の頂点 Quadの右上の位置
new Vector3( hsize, -hsize, 0f), // 3つ目の頂点 Quadの右下の位置
new Vector3(-hsize, -hsize, 0f) // 4つ目の頂点 Quadの左下の位置
};
// Quadのuv座標データ
var uv = new Vector2[] {
new Vector2(0f, 0f), // 1つ目の頂点のuv座標
new Vector2(1f, 0f), // 2つ目の頂点のuv座標
new Vector2(1f, 1f), // 3つ目の頂点のuv座標
new Vector2(0f, 1f) // 4つ目の頂点のuv座標
};
// Quadの法線データ
var normals = new Vector3[] {
new Vector3(0f, 0f, -1f), // 1つ目の頂点の法線
new Vector3(0f, 0f, -1f), // 2つ目の頂点の法線
new Vector3(0f, 0f, -1f), // 3つ目の頂点の法線
new Vector3(0f, 0f, -1f) // 4つ目の頂点の法線
};
次に、モデルの面を表す三角形データを生成します。三角形データは整数配列によって指定され、それぞれの整数は頂点配列のindexに対応しています。
// Quadの面データ 頂点のindexを3つ並べて1つの面(三角形)として認識する
var triangles = new int[] {
0, 1, 2, // 1つ目の三角形
2, 3, 0 // 2つ目の三角形
};
最後に生成したデータをMeshのインスタンスに設定していきます。
mesh.vertices = vertices; mesh.uv = uv; mesh.normals = normals; mesh.triangles = triangles; // Meshが占める境界領域を計算する(cullingに必要) mesh.RecalculateBounds(); return mesh;
本章で利用するサンプルコードでは、ProceduralModelingBaseという基底クラスを利用しています。このクラスの継承クラスでは、モデルのパラメータ(例えば、Quadでは横幅と縦幅を表すsize)を変更するたびに新たなMeshインスタンスを生成し、MeshFilterに適用することで、変更結果をすぐさま確認することができます。(Editorスクリプトを利用してこの機能を実現しています。ProceduralModelingEditor.cs)
また、ProceduralModelingMaterialというenum型のパラメータを変更することで、モデルのUV座標や法線方向を可視化することができます。
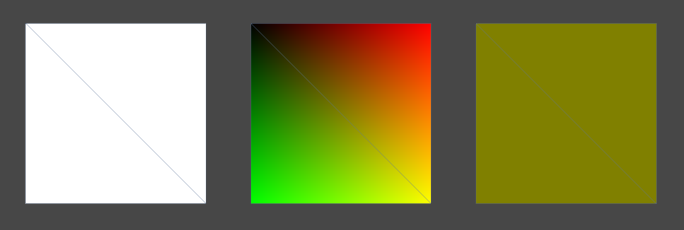
図1.2: 左から、ProceduralModelingMaterial.Standard、ProceduralModelingMaterial.UV、ProceduralModelingMaterial.Normalが適用されたモデル
モデルの構造を理解できたところで、いくつかプリミティブな形状を作っていきましょう。
PlaneはQuadをグリッド上に並べたような形をしています。
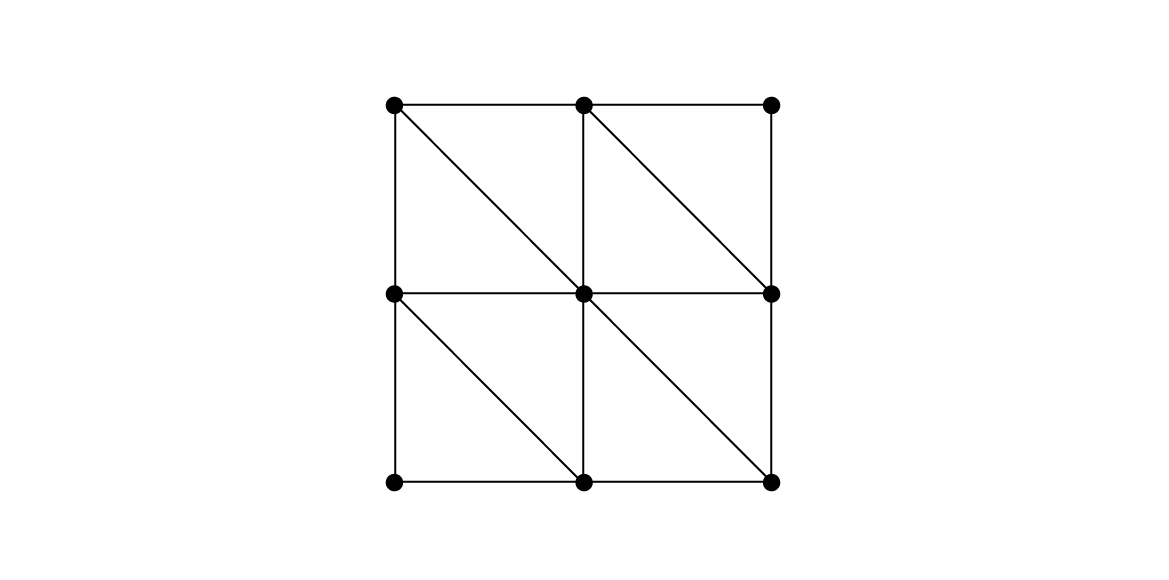
図1.3: Planeモデル
グリッドの行数と列数を決め、それぞれのグリッドの交点に頂点を配置し、グリッドの各マスを埋めるようにQuadを構築し、それらをまとめることで1つのPlaneモデルを生成します。
サンプルプログラムPlane.csでは、Planeの縦に並べる頂点の数heightSegments、横に並べる頂点の数widthSegmentsと、縦の長さheight、横の長さwidthのパラメータを用意しています。それぞれのパラメータは次の図のようにPlaneの形状に影響します。
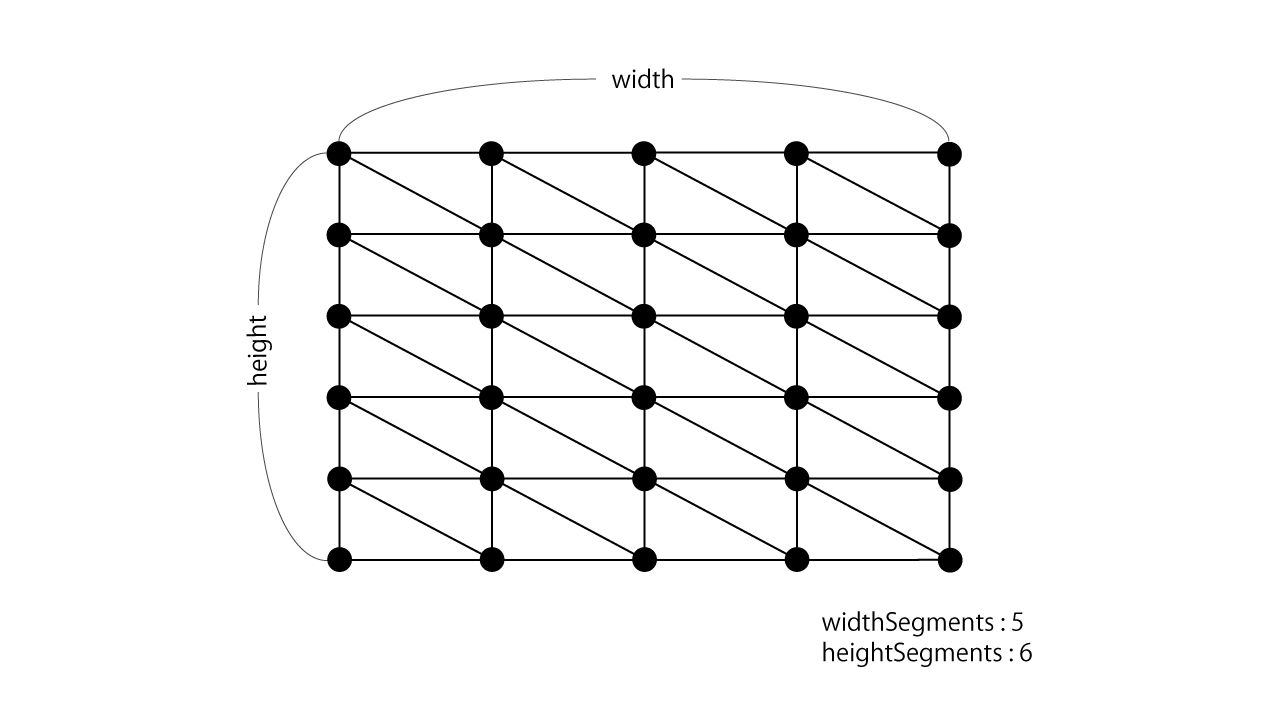
図1.4: Planeパラメータ
まずはグリッドの交点に配置する頂点データを生成していきます。
var vertices = new List<Vector3>();
var uv = new List<Vector2>();
var normals = new List<Vector3>();
// 頂点のグリッド上での位置の割合(0.0 ~ 1.0)を算出するための行列数の逆数
var winv = 1f / (widthSegments - 1);
var hinv = 1f / (heightSegments - 1);
for(int y = 0; y < heightSegments; y++) {
// 行の位置の割合(0.0 ~ 1.0)
var ry = y * hinv;
for(int x = 0; x < widthSegments; x++) {
// 列の位置の割合(0.0 ~ 1.0)
var rx = x * winv;
vertices.Add(new Vector3(
(rx - 0.5f) * width,
0f,
(0.5f - ry) * height
));
uv.Add(new Vector2(rx, ry));
normals.Add(new Vector3(0f, 1f, 0f));
}
}
次に三角形データですが、各三角形に設定する頂点indexは行と列を辿るループの中で、下記のように参照します。
var triangles = new List<int>();
for(int y = 0; y < heightSegments - 1; y++) {
for(int x = 0; x < widthSegments - 1; x++) {
int index = y * widthSegments + x;
var a = index;
var b = index + 1;
var c = index + 1 + widthSegments;
var d = index + widthSegments;
triangles.Add(a);
triangles.Add(b);
triangles.Add(c);
triangles.Add(c);
triangles.Add(d);
triangles.Add(a);
}
}
Planeの各頂点の高さ(y座標)の値は0に設定していましたが、この高さを操作することで、単なる水平な面だけではなく、凸凹した地形や小高い山のような形を得ることができます。
ParametricPlaneBaseクラスはPlaneクラスを継承しており、Meshを生成するBuild関数をoverrideしています。まずは元のPlaneモデルを生成し、各頂点のuv座標をインプットにして高さを求めるDepth(float u, float v)関数を、全ての頂点について呼び出し、高さを設定し直すことで柔軟に形を変形します。
このParametricPlaneBaseクラスを継承したクラスを実装することで、頂点によって高さが変化するPlaneモデルを生成できます。
protected override Mesh Build() {
// 元のPlaneモデルを生成
var mesh = base.Build();
// Planeモデルが持つ頂点の高さを再設定する
var vertices = mesh.vertices;
// 頂点のグリッド上での位置の割合(0.0 ~ 1.0)を算出するための行列数の逆数
var winv = 1f / (widthSegments - 1);
var hinv = 1f / (heightSegments - 1);
for(int y = 0; y < heightSegments; y++) {
// 行の位置の割合(0.0 ~ 1.0)
var ry = y * hinv;
for(int x = 0; x < widthSegments; x++) {
// 列の位置の割合(0.0 ~ 1.0)
var rx = x * winv;
int index = y * widthSegments + x;
vertices[index].y = Depth(rx, ry);
}
}
// 頂点位置の再設定
mesh.vertices = vertices;
mesh.RecalculateBounds();
// 法線方向を自動算出
mesh.RecalculateNormals();
return mesh;
}
サンプルシーンParametricPlane.sceneでは、このParametricPlaneBaseを継承したクラス(MountainPlane、TerrainPlaneクラス)を利用したGameObjectが配置してあります。それぞれのパラメータを変えながら、形が変化していく様子を確認してみてください。

図1.5: ParametricPlane.scene 左がMountainPlaneクラス、右がTerrainPlaneクラスによって生成されたモデル
Cylinderは円筒型のモデルで、次の図のような形をしています。
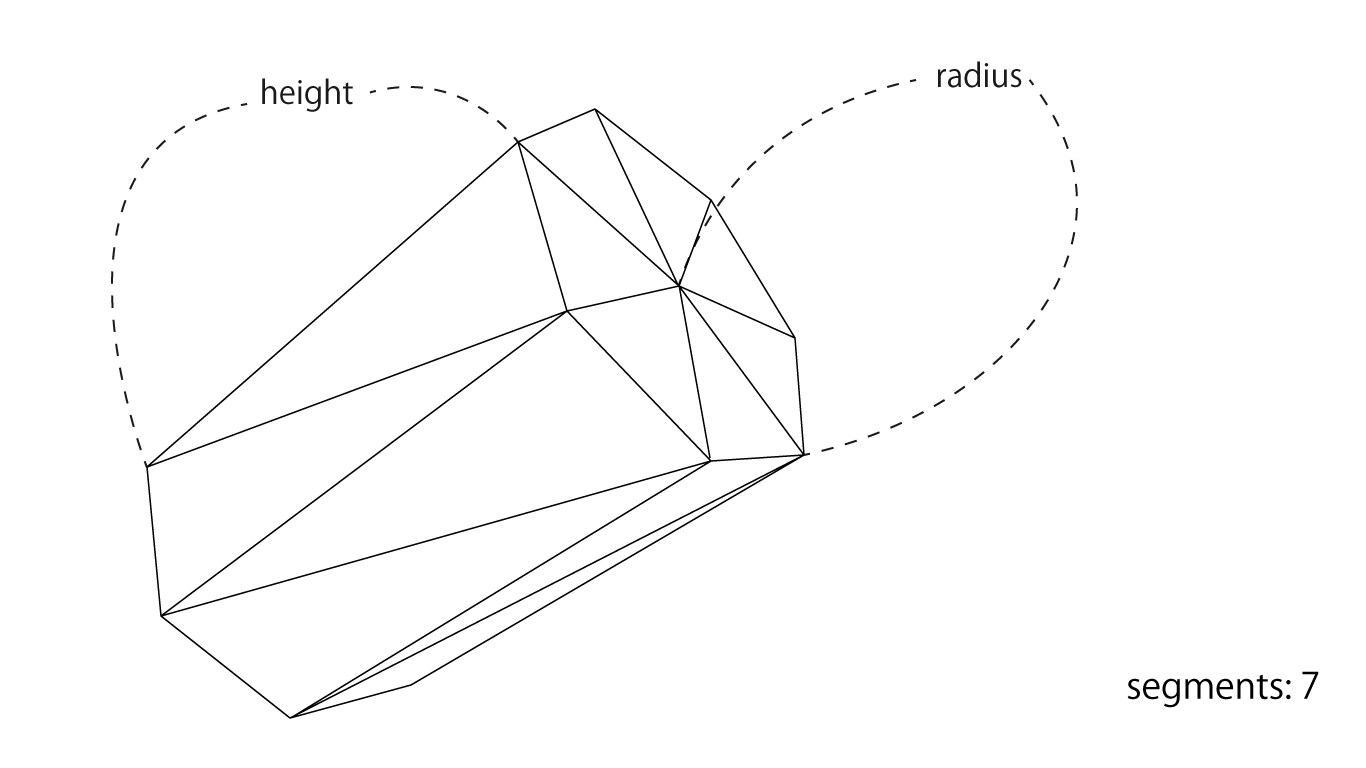
図1.6: Cylinderの構造
円筒型の円のなめらかさはsegments、縦の長さと太さはそれぞれheightとradiusパラメータで制御することができます。上図の例のように、segmentsに7を指定するとCylinderは正7角形を縦に引き伸ばしたような形になり、segmentsの数値を大きくするほど円形に近づいていきます。
Cylinderの頂点は、筒の端に位置する円の周りに沿って均等に並べる必要があります。
円周に沿って均等に並ぶ頂点を配置するには、三角関数(Mathf.Sin, Mathf.Cos)を利用します。ここでは三角関数の詳細については割愛しますが、これらの関数を利用すると角度を元に円周上の位置を得ることができます。
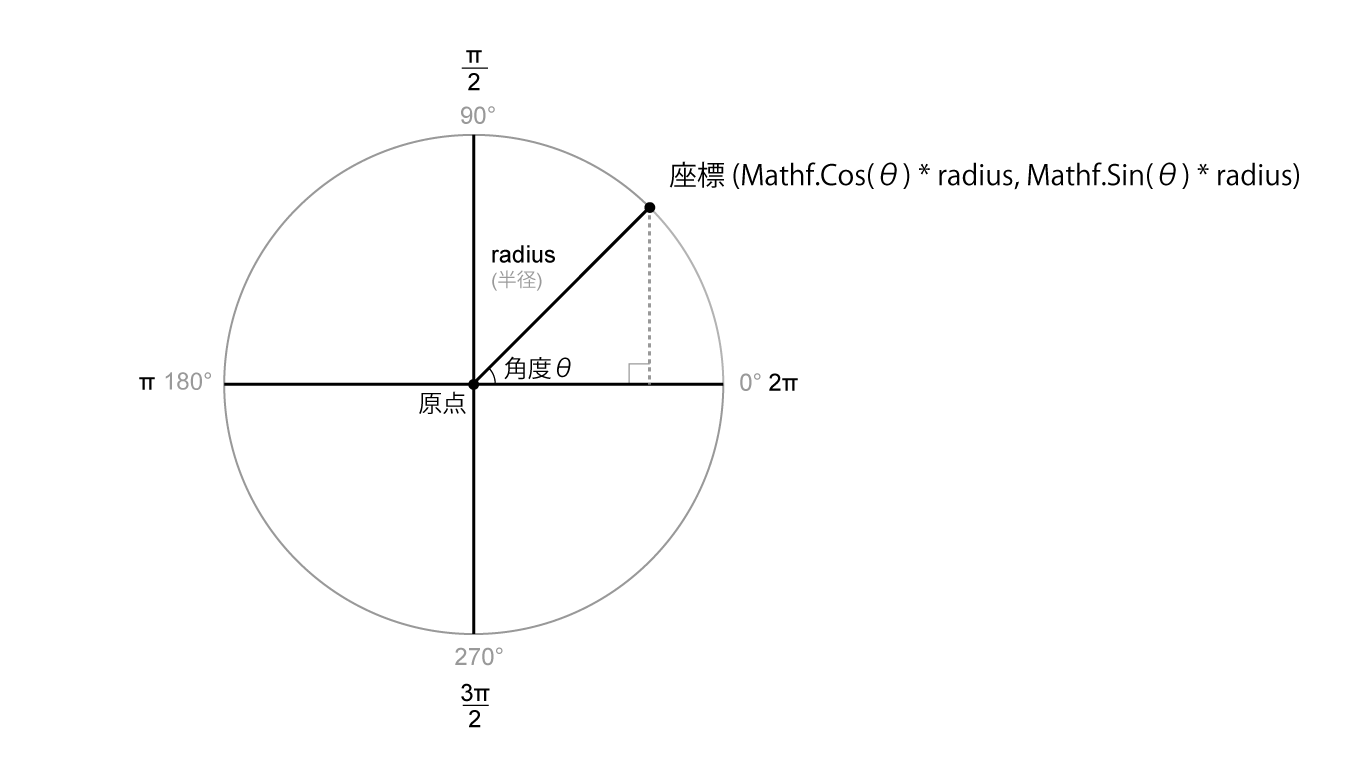
図1.7: 三角関数から円周上の点の位置を得る
この図のように角度θ(シータ)から半径radiusの円上に位置する点は、(x, y) = (Mathf.Cos(θ) * radius, Mathf.Sin(θ) * radius)で取得することができます。
これを元に、半径radiusの円周上に均等に並べられたsegments個の頂点位置を得るには以下のような処理を行います。
for (int i = 0; i < segments; i++) {
// 0.0 ~ 1.0
float ratio = (float)i / (segments - 1);
// [0.0 ~ 1.0]を[0.0 ~ 2π]に変換
float rad = ratio * PI2;
// 円周上の位置を得る
float cos = Mathf.Cos(rad), sin = Mathf.Sin(rad);
float x = cos * radius, y = sin * radius;
}
Cylinderのモデリングでは、円筒の端に位置する円周に沿って均等に頂点を配置し、それらの頂点をつなぎ合わせて側面を形作ります。側面の1つ1つはQuadを構築するのと同じように、上端と下端から対応する頂点を2つずつ取り出して三角形を向かい合わせて配置し、1つの側面、つまり四角形を構築します。Cylinderの側面は、Quadが円形に沿って配置されているものだとイメージできます。
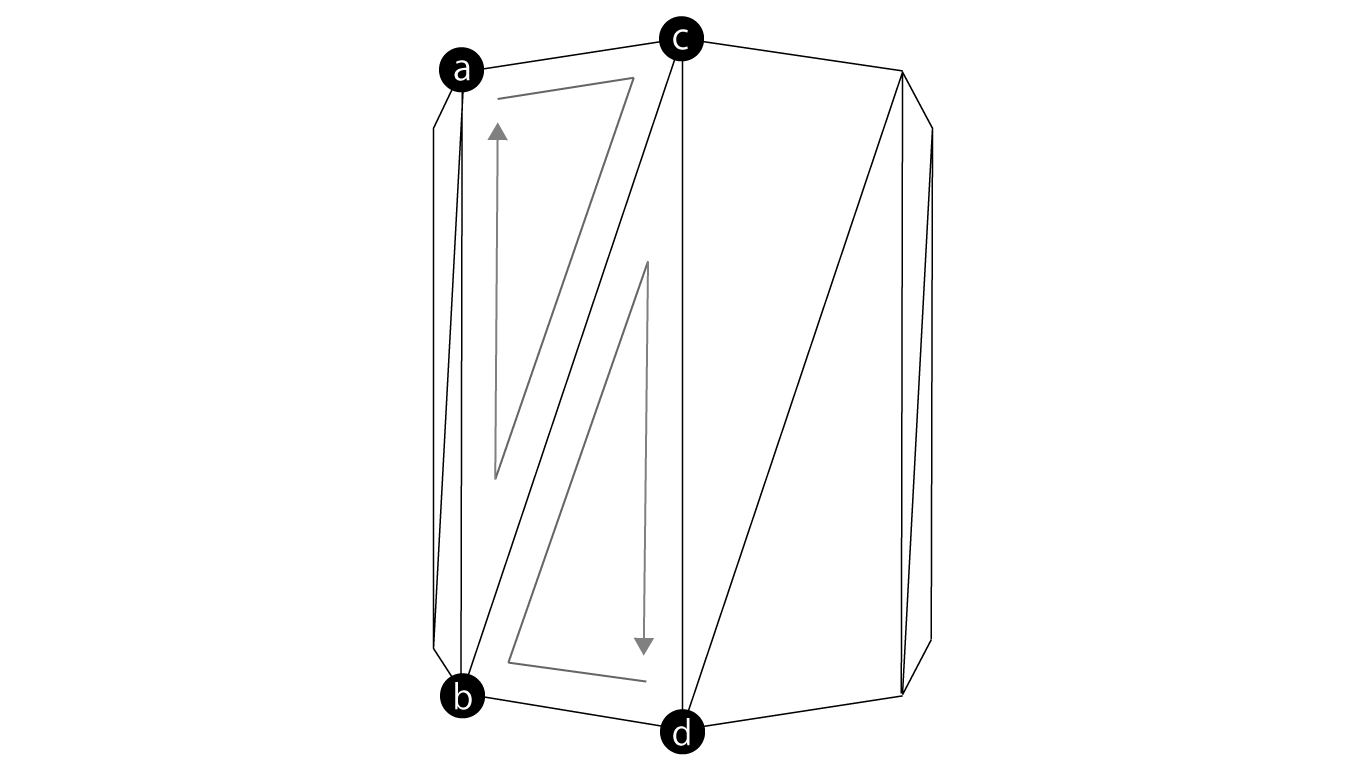
図1.8: Cylinderの側面のモデリング 黒丸は端に位置する円周に沿って均等に配置された頂点 頂点内のa〜dはCylinder.csプログラム内で三角形を構築する際に頂点に割り振られるindex変数
まずは側面を構築していきますが、Cylinderクラスでは上端と下端に位置する円周に並べられた頂点のデータを生成するための関数GenerateCapを用意しています。
var vertices = new List<Vector3>();
var normals = new List<Vector3>();
var uvs = new List<Vector2>();
var triangles = new List<int>();
// 上端の高さと、下端の高さ
float top = height * 0.5f, bottom = -height * 0.5f;
// 側面を構成する頂点データを生成
GenerateCap(segments + 1, top, bottom, radius, vertices, uvs, normals, true);
// 側面の三角形を構築する際、円上の頂点を参照するために、
// indexが円を一周するための除数
var len = (segments + 1) * 2;
// 上端と下端をつなぎ合わせて側面を構築
for (int i = 0; i < segments + 1; i++) {
int idx = i * 2;
int a = idx, b = idx + 1, c = (idx + 2) % len, d = (idx + 3) % len;
triangles.Add(a);
triangles.Add(c);
triangles.Add(b);
triangles.Add(d);
triangles.Add(b);
triangles.Add(c);
}
GenerateCap関数では、List型で渡された変数に頂点や法線データを設定します。
void GenerateCap(
int segments,
float top,
float bottom,
float radius,
List<Vector3> vertices,
List<Vector2> uvs,
List<Vector3> normals,
bool side
) {
for (int i = 0; i < segments; i++) {
// 0.0 ~ 1.0
float ratio = (float)i / (segments - 1);
// 0.0 ~ 2π
float rad = ratio * PI2;
// 円周に沿って上端と下端に均等に頂点を配置する
float cos = Mathf.Cos(rad), sin = Mathf.Sin(rad);
float x = cos * radius, z = sin * radius;
Vector3 tp = new Vector3(x, top, z), bp = new Vector3(x, bottom, z);
// 上端
vertices.Add(tp);
uvs.Add(new Vector2(ratio, 1f));
// 下端
vertices.Add(bp);
uvs.Add(new Vector2(ratio, 0f));
if(side) {
// 側面の外側を向く法線
var normal = new Vector3(cos, 0f, sin);
normals.Add(normal);
normals.Add(normal);
} else {
normals.Add(new Vector3(0f, 1f, 0f)); // 蓋の上を向く法線
normals.Add(new Vector3(0f, -1f, 0f)); // 蓋の下を向く法線
}
}
}
Cylinderクラスでは、上端と下端を閉じたモデルにするかどうかをopenEndedフラグで設定することができます。上端と下端を閉じる場合は、円形の「蓋」を形作り、端に栓をします。
蓋の面を構成する頂点は、側面を構成している頂点を利用せずに、側面と同じ位置に別途新しく頂点を生成します。これは、側面と蓋の部分とで法線を分け、自然なライティングを施すためです。(側面の頂点データを構築する場合はGenerateCapの引数のside変数にtrueを、蓋を構築する場合はfalseを指定し、適切な法線方向が設定されるようにしています。)
もし、側面と蓋の部分で同じ頂点を共有してしまうと、側面と蓋面で同じ法線を参照することになってしまうので、ライティングが不自然になってしまいます。

図1.9: Cylinderの側面と蓋の頂点を共有した場合(左:BadCylinder.cs)と、サンプルプログラムのように別の頂点を用意した場合(右:Cylinder.cs) 左はライティングが不自然になっている
円形の蓋をモデリングするには、(GenerateCap関数から生成される)円周上に均等に並べられた頂点と、円の真ん中に位置する頂点を用意し、真ん中の頂点から円周に沿った頂点をつなぎ合わせて、均等に分けられたピザのように三角形を構築することで円形の蓋を形作ります。
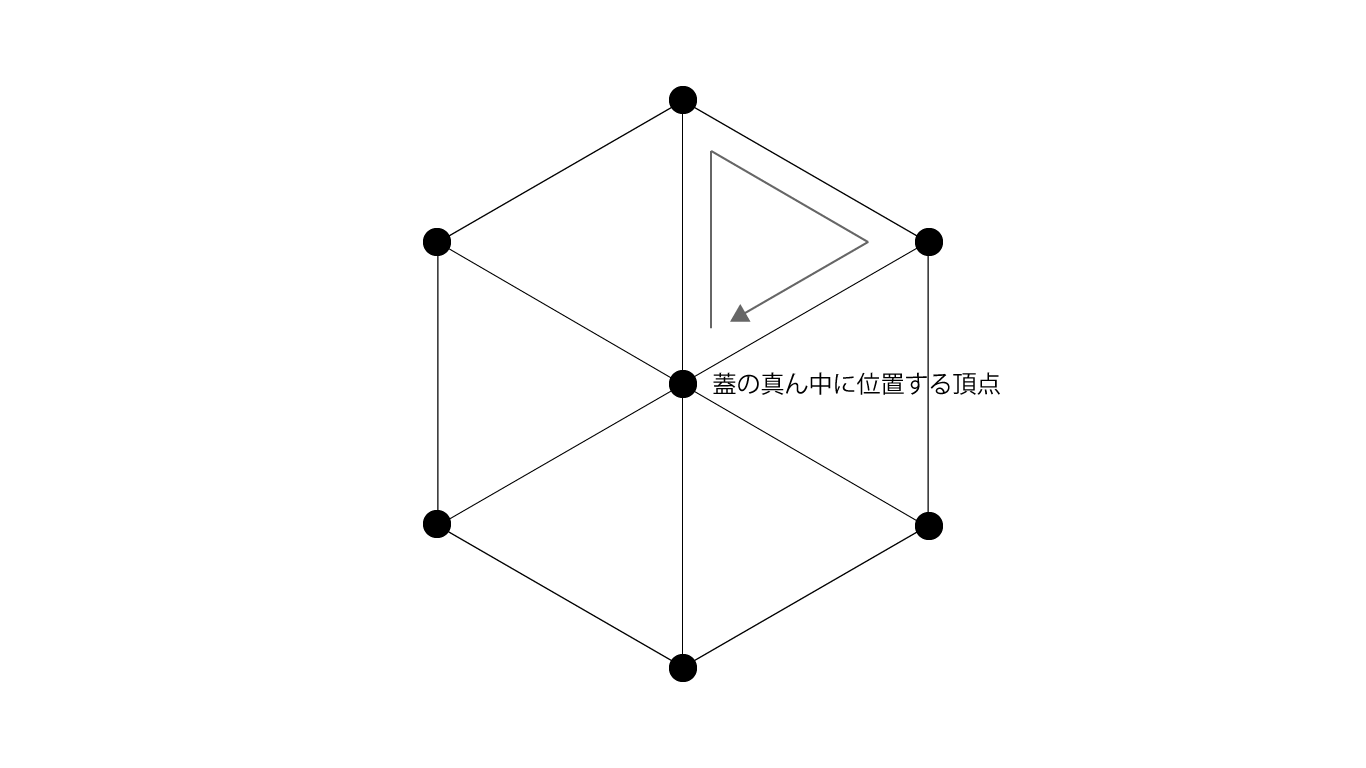
図1.10: Cylinderの蓋のモデリング segmentsパラメータが6の場合の例
// 上端と下端の蓋を生成
if(openEnded) {
// 蓋のモデルのための頂点は、ライティング時に異なった法線を利用するために、側面とは共有せずに新しく追加する
GenerateCap(
segments + 1,
top,
bottom,
radius,
vertices,
uvs,
normals,
false
);
// 上端の蓋の真ん中の頂点
vertices.Add(new Vector3(0f, top, 0f));
uvs.Add(new Vector2(0.5f, 1f));
normals.Add(new Vector3(0f, 1f, 0f));
// 下端の蓋の真ん中の頂点
vertices.Add(new Vector3(0f, bottom, 0f)); // bottom
uvs.Add(new Vector2(0.5f, 0f));
normals.Add(new Vector3(0f, -1f, 0f));
var it = vertices.Count - 2;
var ib = vertices.Count - 1;
// 側面の分の頂点indexを参照しないようにするためのoffset
var offset = len;
// 上端の蓋の面
for (int i = 0; i < len; i += 2) {
triangles.Add(it);
triangles.Add((i + 2) % len + offset);
triangles.Add(i + offset);
}
// 下端の蓋の面
for (int i = 1; i < len; i += 2) {
triangles.Add(ib);
triangles.Add(i + offset);
triangles.Add((i + 2) % len + offset);
}
}
Tubularは筒型のモデルで、次の図のような形をしています。

図1.11: Tubularモデル
Cylinderモデルはまっすぐに伸びる円筒形状ですが、Tubularは曲線に沿ったねじれのない筒型をしています。後述する樹木モデルの例では、一本の枝をTubularで表現し、その組み合わせで一本の木を構築する手法を採用しているのですが、滑らかに曲がる筒型が必要な場面でTubularは活躍します。
筒型モデルの構造は次の図のようになっています。
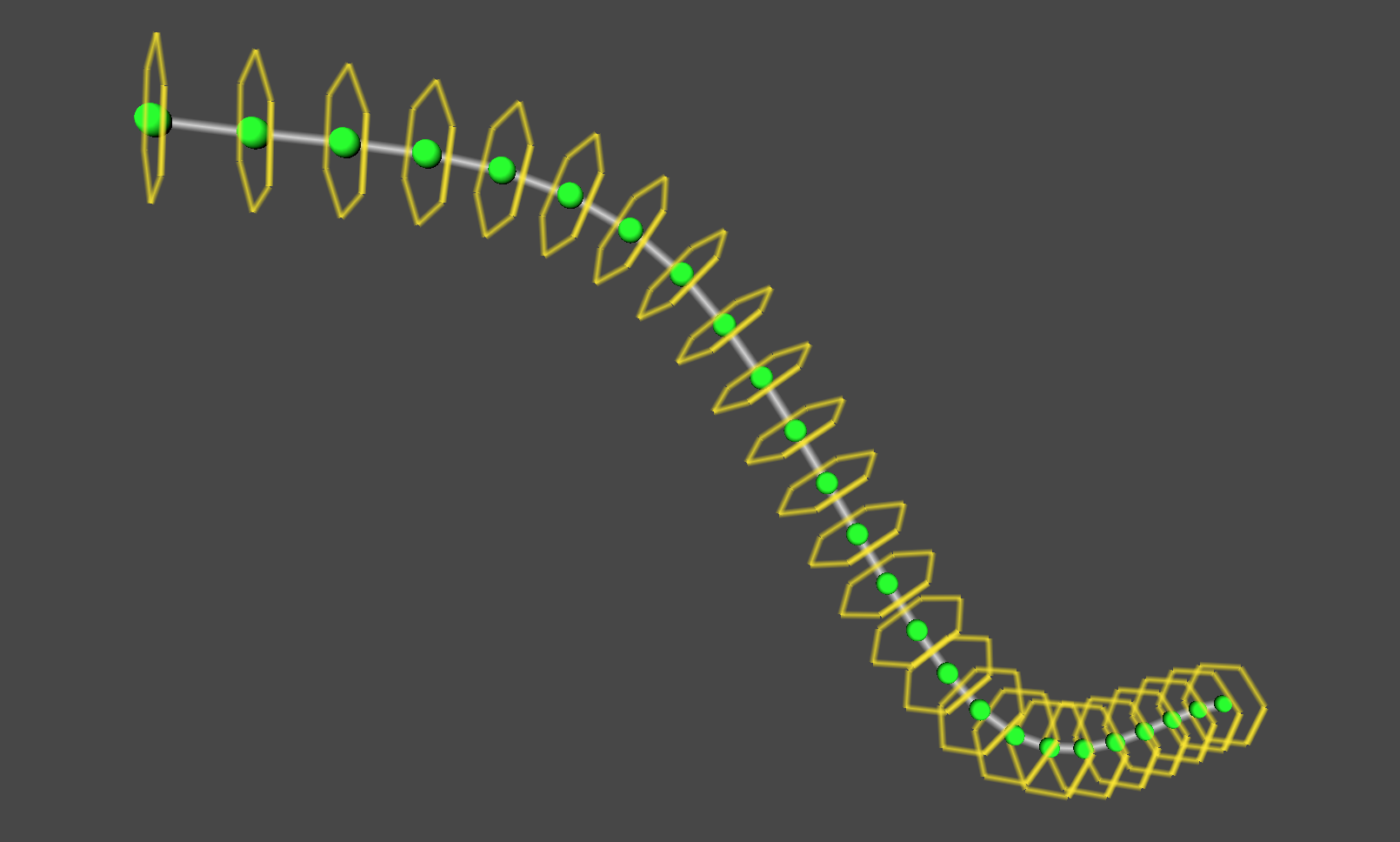
図1.12: 筒型の構造 Tubularが沿う曲線を分割する点を球で、側面を構成する節を六角形で可視化している
曲線を分割し、分割点によって区切られた節ごとに側面を構築していき、それらを組み合わせることで1つのTubularモデルを生成します。
1つ1つの節の側面はCylinderの側面と同じように、側面の上端と下端の頂点を円形に沿って均等に配置し、それらをつなぎ合わせて構築するため、Cylinderを曲線に沿って連結したものがTubular型だと考えることができます。
サンプルプログラムでは、曲線を表す基底クラスCurveBaseを用意しています。3次元空間上の曲線の描き方については、様々なアルゴリズムが考案されており、用途に応じて使いやすい手法を選択する必要があります。サンプルプログラムでは、CurveBaseクラスを継承したクラスCatmullRomCurveを利用しています。
ここでは詳細は割愛しますが、CatmullRomCurveは渡された制御点全てを通るように点と点の間を補間しつつ曲線を形作るという特徴があり、曲線に経由させたい点を指定できるため、使い勝手の良さに定評があります。
曲線を表すCurveBaseクラスでは、曲線上の点の位置と傾き(tangentベクトル)を得るためにGetPointAt(float)・GetTangentAt(float)関数を用意しており、引数に[0.0 ~ 1.0]の値を指定することで、始点(0.0)から終点(1.0)の間にある点の位置と傾きを取得できます。
曲線に沿ったねじれのない筒型を作るには、曲線に沿ってなめらかに変化する3つの直交するベクトル「接線(tangent)ベクトル、法線(normal)ベクトル、従法線(binormal)ベクトル」の配列が必要となります。接線ベクトルは、曲線上の一点における傾きを表す単位ベクトルのことで、法線ベクトルと従法線ベクトルはお互いに直交するベクトルとして求めます。
これらの直交するベクトルによって、曲線上のある一点において「曲線に直交する円周上の座標」を得ることができます。
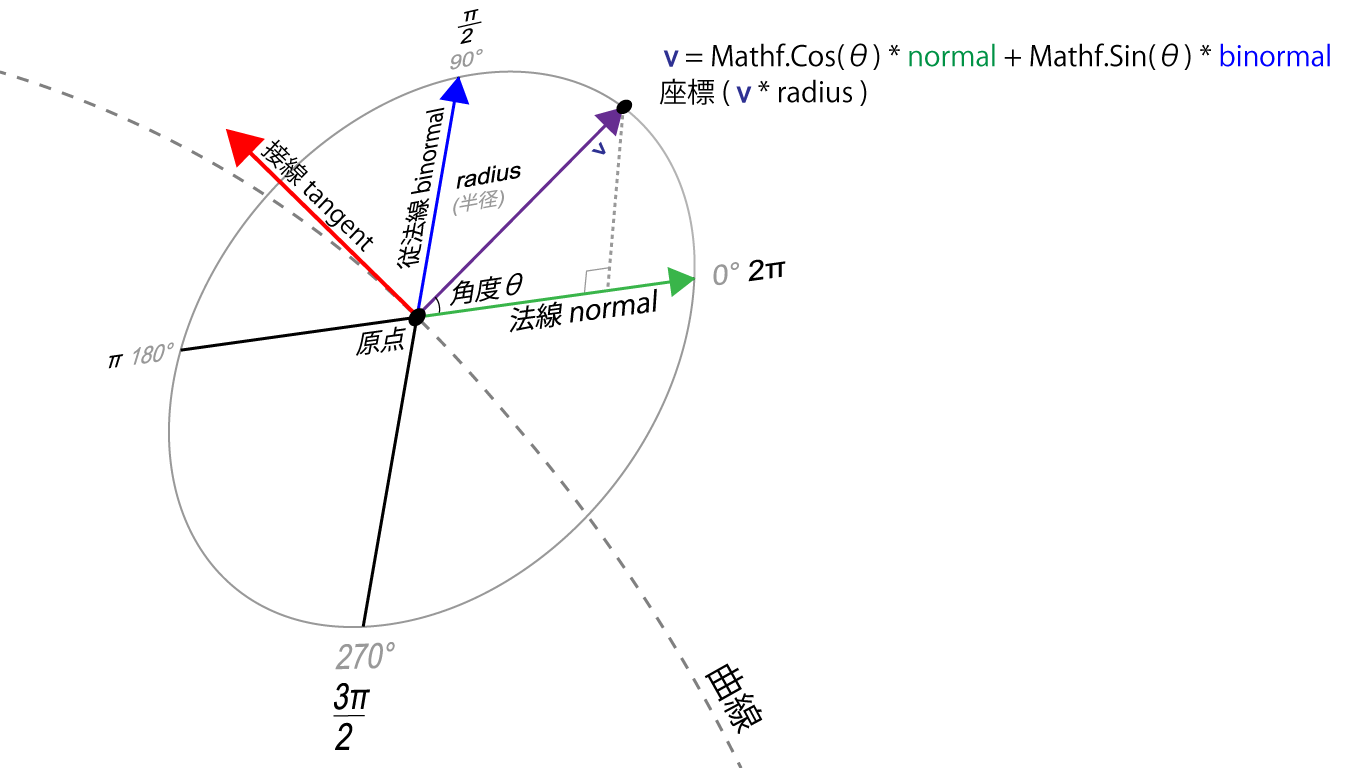
図1.13: 法線(normal)と従法線(binormal)から、円周上の座標を指す単位ベクトル(v)を求める この単位ベクトル(v)に半径radiusを乗算することで、曲線に直交する半径radiusの円周上の座標を得ることができる
この曲線上のある一点における3つの直交するベクトルの組のことをFrenet frame(フレネフレーム)と呼びます。

図1.14: Tubularを構成するFrenet frame配列の可視化 枠が1つのFrenet frameを表し、3つの矢印は接線(tangent)ベクトル、法線(normal)ベクトル、従法線(binormal)ベクトルを示している
Tubularのモデリングは、このFrenet frameから得られた法線と従法線を元に節ごとの頂点データを求め、それらをつなぎ合わせていくという手順で行います。
サンプルプログラムでは、CurveBaseクラスがこのFrenet frame配列を生成するための関数ComputeFrenetFramesを持っています。
Tubularクラスは曲線を表すCatmullRomCurveクラスを持ち、このCatmullRomCurveが描く曲線に沿って筒型を形成します。
CatmullRomCurveクラスは4つ以上の制御点が必要で、制御点を操作すると曲線の形状が変化し、それに伴ってTubularモデルの形状も変化していきます。
var vertices = new List<Vector3>();
var normals = new List<Vector3>();
var tangents = new List<Vector4>();
var uvs = new List<Vector2>();
var triangles = new List<int>();
// 曲線からFrenet frameを取得
var frames = curve.ComputeFrenetFrames(tubularSegments, closed);
// Tubularの頂点データを生成
for(int i = 0; i < tubularSegments; i++) {
GenerateSegment(curve, frames, vertices, normals, tangents, i);
}
// 閉じた筒型を生成する場合は曲線の始点に最後の頂点を配置し、閉じない場合は曲線の終点に配置する
GenerateSegment(
curve,
frames,
vertices,
normals,
tangents,
(!closed) ? tubularSegments : 0
);
// 曲線の始点から終点に向かってuv座標を設定していく
for (int i = 0; i <= tubularSegments; i++) {
for (int j = 0; j <= radialSegments; j++) {
float u = 1f * j / radialSegments;
float v = 1f * i / tubularSegments;
uvs.Add(new Vector2(u, v));
}
}
// 側面を構築
for (int j = 1; j <= tubularSegments; j++) {
for (int i = 1; i <= radialSegments; i++) {
int a = (radialSegments + 1) * (j - 1) + (i - 1);
int b = (radialSegments + 1) * j + (i - 1);
int c = (radialSegments + 1) * j + i;
int d = (radialSegments + 1) * (j - 1) + i;
triangles.Add(a); triangles.Add(d); triangles.Add(b);
triangles.Add(b); triangles.Add(d); triangles.Add(c);
}
}
var mesh = new Mesh();
mesh.vertices = vertices.ToArray();
mesh.normals = normals.ToArray();
mesh.tangents = tangents.ToArray();
mesh.uv = uvs.ToArray();
mesh.triangles = triangles.ToArray();
関数GenerateSegmentは先述したFrenet frameから取り出した法線と従法線を元に、指定された節の頂点データを計算し、List型で渡された変数に設定します。
void GenerateSegment(
CurveBase curve,
List<FrenetFrame> frames,
List<Vector3> vertices,
List<Vector3> normals,
List<Vector4> tangents,
int index
) {
// 0.0 ~ 1.0
var u = 1f * index / tubularSegments;
var p = curve.GetPointAt(u);
var fr = frames[index];
var N = fr.Normal;
var B = fr.Binormal;
for(int j = 0; j <= radialSegments; j++) {
// 0.0 ~ 2π
float rad = 1f * j / radialSegments * PI2;
// 円周に沿って均等に頂点を配置する
float cos = Mathf.Cos(rad), sin = Mathf.Sin(rad);
var v = (cos * N + sin * B).normalized;
vertices.Add(p + radius * v);
normals.Add(v);
var tangent = fr.Tangent;
tangents.Add(new Vector4(tangent.x, tangent.y, tangent.z, 0f));
}
}
この節では、これまで説明したProceduralModelingのテクニックを使って、より複雑なモデルを生成する手法について紹介します。
植物のモデリングは、ProceduralModelingのテクニックの応用例としてよく取り上げられています。Unity内でも樹木をEditor内でモデリングするためのTree API*4が用意されていますし、Speed Tree*5という植物のモデリング専用のソフトが存在します。
[*4] https://docs.unity3d.com/ja/540/Manual/tree-FirstTree.html
[*5] http://www.speedtree.com/
この節では、植物の中でも比較的モデリング手法が単純な樹木のモデリングについて取り上げます。
植物の構造を記述・表現できるアルゴリズムとしてL-Systemがあります。L-Systemは植物学者であるAristid Lindenmayerによって1968年に提唱されたもので、L-SystemのLは彼の名前から来ています。
L-Systemを用いると、植物の形状に見られる自己相似性を表現することができます。
自己相似性とは、物体の細部の形を拡大してみると、大きなスケールで見たその物体の形と一致することで、例えば樹木の枝分かれを観察すると、幹に近い部分の枝の分かれ方と、先端に近い部分の枝の分かれ方に相似性があります。
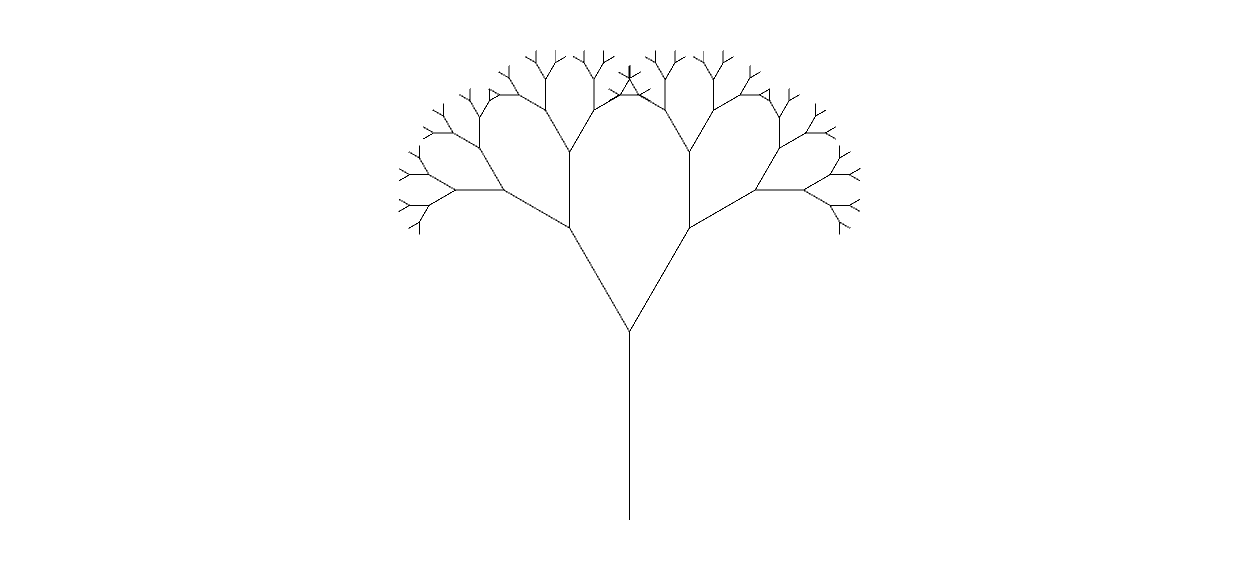
図1.15: それぞれの枝が30度ずつの変化で枝分かれした図形 根元の部分と枝先の部分で相似になっていることがわかるが、このようなシンプルな図形でも樹木のような形に見える(サンプルプログラム LSystem.scene)
L-Systemは、要素を記号で表し、記号を置き換える規則を定め、記号に対して規則を繰り返し適用していくことで、記号の列を複雑に発展させていくメカニズムを提供します。
例えば簡単な例をあげると、
を
に従って書き換えていくと、
a -> ab -> aba -> abaab -> abaababa -> ...
という風にステップを経るごとに複雑な結果を生み出します。
このL-Systemをグラフィック生成に利用した例がサンプルプログラムのLSystemクラスです。
LSystemクラスでは、以下の操作
を用意しており、
を
に従って、決まられた回数だけ規則の適用を繰り返しています。
その結果、サンプルのLSystem.sceneに示すような、自己相似性を持つ図を描くことができます。このL-Systemの持つ「状態を再帰的に書き換えていく」という性質が自己相似性を生み出すのです。自己相似性はFractal(フラクタル)とも呼ばれ、1つの研究分野にもなっています。
実際にL-Systemを樹木のモデルを生成するプログラムに応用した例として、ProceduralTreeというクラスを用意しました。
ProceduralTreeでは、前項で解説したLSystemクラスと同様に「枝を進めては分岐し、さらに枝を進める」というルーチンを再帰的に呼び出すことで木の形を生成していきます。
前項のLSystemクラスでは、枝の分岐に関しては「一定角度、左と右の二方向に分岐する」という単純なルールでしたが、ProceduralTreeでは乱数を用い、分岐する数や分岐方向にランダム性を持たせ、枝が複雑に分岐するようなルールを設定しています。

図1.16: ProceduralTree.scene
TreeDataクラスは枝の分岐具合を定めるパラメータや、木のサイズ感やモデルのメッシュの細かさを決めるパラメータを内包したクラスです。このクラスのインスタンスのパラメータを調整することで、木の形をデザインすることができます。
TreeDataクラス内のいくつかのパラメータを用いて枝の分かれ具合を調整します。
1つの枝から分岐する枝の数はbranchesMin・branchesMaxパラメータで調整します。branchesMinが分岐する枝の最小数、branchesMaxが分岐する枝の最大数を表しており、branchesMinからbranchesMaxの間の数をランダムに選び、分岐する数を決めます。
分岐する枝が生える方向はgrowthAngleMin・growthAngleMaxパラメータで調整します。growthAngleMinは分岐する方向の最小角度、growthAngleMaxが最大角度を表しており、growthAngleMinからgrowthAngleMaxの間の数をランダムに選び、分岐する方向を決めます。
それぞれの枝は伸びる方向を表すtangentベクトルと、それと直交するベクトルとしてnormalベクトルとbinormalベクトルを持ちます。
growthAngleMin・growAngleMaxパラメータからランダムに得られた値は、分岐点から伸びる方向のtangentベクトルに対して、normalベクトルの方向とbinormalベクトルの方向に回転が加えられます。
分岐点から伸びる方向tangentベクトルに対してランダムな回転を加えることで、分岐先の枝が生える方向を変化させ、枝分かれを複雑に変化させます。
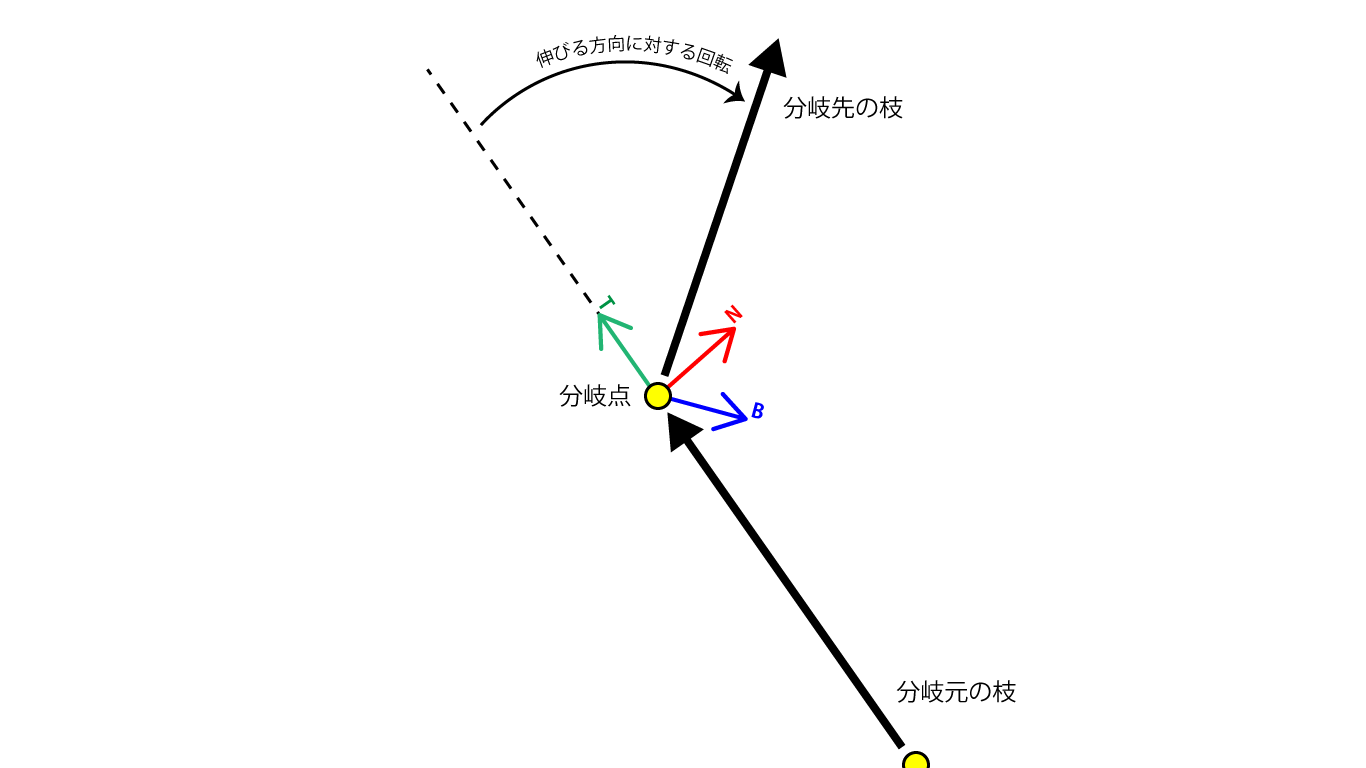
図1.17: 分岐点から伸びる方向に対してかけられるランダムな回転 分岐点でのTの矢印は伸びる方向(tangentベクトル)、Nの矢印は法線(normalベクトル)、Bの矢印は従法線(binormalベクトル)を表し、伸びる方向に対して法線と従法線の方向にランダムな回転がかけられる
枝が生える方向にランダムにかけられる回転の角度が枝先にいくほど大きくなるようにgrowthAngleScaleパラメータを用意しています。このgrowthAngleScaleパラメータは、枝のインスタンスが持つ世代を表すgenerationパラメータが0に近づくほど、つまり枝先に近づくほど、回転する角度に強く影響し、回転の角度を大きくします。
// 枝先ほど分岐する角度が大きくなる
var scale = Mathf.Lerp(
1f,
data.growthAngleScale,
1f - 1f * generation / generations
);
// normal方向の回転
var qn = Quaternion.AngleAxis(scale * data.GetRandomGrowthAngle(), normal);
// binormal方向の回転
var qb = Quaternion.AngleAxis(scale * data.GetRandomGrowthAngle(), binormal);
// 枝先が向いているtangent方向にqn * qbの回転をかけつつ、枝先の位置を決める
this.to = from + (qn * qb) * tangent * length;
枝はTreeBranchクラスで表現されます。
世代数(generations)と基本となる長さ(length)と太さ(radius)のパラメータに加えて、分岐パターンを設定するためのTreeDataを引数に指定してコンストラクタを呼び出すと、内部で再帰的にTreeBranchのインスタンスが生成されていきます。
1つのTreeBranchから分岐したTreeBranchは、元のTreeBranch内にあるList<TreeBranch>型であるchildren変数に格納され、根元のTreeBranchから全ての枝に辿れるようにしています。
一本の枝のモデルは、Tubular同様、一本の曲線を分割し、分割された節を1つのCylinderとしてモデル化し、それらをつなぎ合わせていくように構築していきます。
TreeSegmentクラスは一本の曲線を分割する節(Segment)を表現するクラスです。
public class TreeSegment {
public FrenetFrame Frame { get { return frame; } }
public Vector3 Position { get { return position; } }
public float Radius { get { return radius; } }
// TreeSegmentが向いている方向ベクトルtangent、
// それと直交するベクトルnormal、binormalを持つFrenetFrame
FrenetFrame frame;
// TreeSegmentの位置
Vector3 position;
// TreeSegmentの幅(半径)
float radius;
public TreeSegment(FrenetFrame frame, Vector3 position, float radius) {
this.frame = frame;
this.position = position;
this.radius = radius;
}
}
1つのTreeSegmentは節が向いている方向のベクトルと直交ベクトルがセットになったFrenetFrame、位置と幅を表す変数を持ち、Cylinderを構築する際の上端と下端に必要な情報を保持します。
ProceduralTreeのモデル生成ロジックはTubularを応用したもので、一本の枝TreeBranchが持つTreeSegmentの配列からTubularモデルを生成し、それらを1つのモデルに集約することで全体の一本の木を形作る、というアプローチでモデリングしています。
var root = new TreeBranch(
generations,
length,
radius,
data
);
var vertices = new List<Vector3>();
var normals = new List<Vector3>();
var tangents = new List<Vector4>();
var uvs = new List<Vector2>();
var triangles = new List<int>();
// 木の全長を取得
// 枝の長さを全長で割ることで、uv座標の高さ(uv.y)が
// 根元から枝先に至るまで[0.0 ~ 1.0]で変化するように設定する
float maxLength = TraverseMaxLength(root);
// 再帰的に全ての枝を辿り、1つ1つの枝に対応するMeshを生成する
Traverse(root, (branch) => {
var offset = vertices.Count;
var vOffset = branch.Offset / maxLength;
var vLength = branch.Length / maxLength;
// 一本の枝から頂点データを生成する
for(int i = 0, n = branch.Segments.Count; i < n; i++) {
var t = 1f * i / (n - 1);
var v = vOffset + vLength * t;
var segment = branch.Segments[i];
var N = segment.Frame.Normal;
var B = segment.Frame.Binormal;
for(int j = 0; j <= data.radialSegments; j++) {
// 0.0 ~ 2π
var u = 1f * j / data.radialSegments;
float rad = u * PI2;
float cos = Mathf.Cos(rad), sin = Mathf.Sin(rad);
var normal = (cos * N + sin * B).normalized;
vertices.Add(segment.Position + segment.Radius * normal);
normals.Add(normal);
var tangent = segment.Frame.Tangent;
tangents.Add(new Vector4(tangent.x, tangent.y, tangent.z, 0f));
uvs.Add(new Vector2(u, v));
}
}
// 一本の枝の三角形を構築する
for (int j = 1; j <= data.heightSegments; j++) {
for (int i = 1; i <= data.radialSegments; i++) {
int a = (data.radialSegments + 1) * (j - 1) + (i - 1);
int b = (data.radialSegments + 1) * j + (i - 1);
int c = (data.radialSegments + 1) * j + i;
int d = (data.radialSegments + 1) * (j - 1) + i;
a += offset;
b += offset;
c += offset;
d += offset;
triangles.Add(a); triangles.Add(d); triangles.Add(b);
triangles.Add(b); triangles.Add(d); triangles.Add(c);
}
}
});
var mesh = new Mesh();
mesh.vertices = vertices.ToArray();
mesh.normals = normals.ToArray();
mesh.tangents = tangents.ToArray();
mesh.uv = uvs.ToArray();
mesh.triangles = triangles.ToArray();
mesh.RecalculateBounds();
植物のプロシージャルモデリングは樹木だけでも奥深く、日光の照射率が高くなるように枝分かれすることで自然な木のモデルを得るようにする、といった手法などが考案されています。
こうした植物のモデリングに興味がある方はL-Systemを考案したAristid Lindenmayerにより執筆されたThe Algorithmic Beauty of Plants*6に様々な手法が紹介されていますので、参考にしてみてください。
[*6] http://algorithmicbotany.org/papers/#abop
これまで紹介したプロシージャルモデリングの例から、「モデルをパラメータによって変化させながら動的に生成できる」というテクニックの利点を知ることができました。効率的に様々なバリエーションのモデルを作成できるため、コンテンツ開発の効率化のための技術という印象を受けるかもしれません。
しかし、世の中にあるモデリングツールやスカルプトツールのように、プロシージャルモデリングのテクニックは「ユーザの入力に応じて、インタラクティブにモデルを生成する」という応用も可能です。
応用例として、東京大学大学院情報工学科の五十嵐健夫氏により考案された、手書きスケッチによる輪郭線から立体モデルを生成する技術「Teddy」についてご紹介します。

図1.18: 手書きスケッチによる3次元モデリングを行う技術「Teddy」のUnityアセット http://uniteddy.info/ja
2002年にプレイステーション2用のソフトとして発売された「ガラクタ名作劇場 ラクガキ王国」*7というゲームでは実際にこの技術が用いられ、「自分の描いた絵を3D化してゲーム内のキャラクターとして動かす」という応用が実現されています。
[*7] https://ja.wikipedia.org/wiki/ラクガキ王国
この技術では、
[*8] https://en.wikipedia.org/wiki/Delaunay_triangulation
という手順で3次元モデルを生成しています。アルゴリズムの詳細に関してはコンピュータグラフィクスを扱う国際会議SIGGRAPHにて発表された論文が公開されています。*9
[*9] http://www-ui.is.s.u-tokyo.ac.jp/~takeo/papers/siggraph99.pdf
TeddyはUnityに移植されたバージョンがAsset Storeに公開されているので、誰でもコンテンツにこの技術を組み込むことができます。*10
[*10] http://uniteddy.info/ja/
このようにプロシージャルモデリングのテクニックを用いれば、独自のモデリングツールを開発することができ、ユーザの創作によって発展していくようなコンテンツを作ることも可能になります。
プロシージャルモデリングのテクニックを使えば、
が実現できることを見てきました。
Unity自体はゲームエンジンであるため、本章で紹介した例からはゲームや映像コンテンツ内での応用を想像されるでしょう。
しかし、コンピュータグラフィックスの技術自体の応用範囲が広いように、モデルを生成する技術の応用範囲も広いものだと考えることができます。冒頭でも述べましたが、建築やプロダクトデザインの分野でもプロシージャルモデリングの手法が利用されていますし、3Dプリンタ技術などのデジタルファブリケーションの発展にともなって、デザインした形を実生活で利用できる機会が個人レベルでも増えてきています。
このように、どのような分野でデザインした形を利用するかを広い視野で考えると、プロシージャルモデリングのテクニックを応用できる場面が様々なところから見つかるかもしれません。